Basarab-Horwath 1991 proposition 2
See @basarab
Let
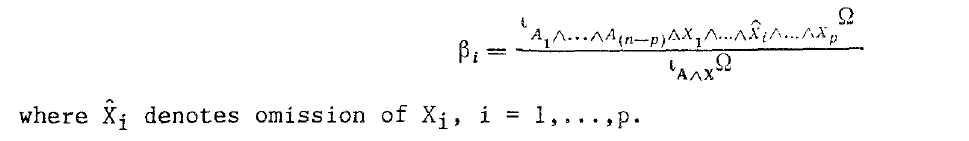
The form $\beta_i$ is closed if and only if the system $\{A,X_1,\ldots,\hat{X}_i,\ldots,X_p\}$ is closed and $X_i$ is a symmetry of it
Adaptación a mi contexto
Given a codimension 1 involutive distribution $\mathcal{Z}=\mathcal{S}(Z_1,\ldots,Z_{n-1})$ on a $n$-dimensional manifold $M$ and a vector field $X$ symmetry of $\mathcal{Z}$, the 1-form
$$ \omega=\frac{\left.\left.\left.Z_{n-1}\right\lrcorner \cdots\right\lrcorner Z_1\right\lrcorner \boldsymbol{\Omega}}{\left.\left.\left.X \right \lrcorner Z_{n-1}\right\lrcorner \cdots Z_1\right\lrcorner \boldsymbol{\Omega}} $$where $\boldsymbol{\Omega}$ is a volume form and $\left. \right\lrcorner$ denote contraction, is closed.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: